원문: Non-negative least squares

비음수 최소제곱법

이 예제에서, 우리는 회귀 계수(regression coefficients)에 양수 제약(positive constraints)을 갖는 선형 모델을 적합하고, 추정된 계수(coefficients)를 고전적인 선형 회귀(linear regression)와 비교합니다.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import r2_score

무작위 데이터를 약간 생성합니다.

np.random.seed(42)

n_samples, n_features = 200, 50
X = np.random.randn(n_samples, n_features)
true_coef = 3 * np.random.randn(n_features)
# 계수를 비음수로 보이게끔 임계치를 만듭니다
true_coef[true_coef < 0] = 0
y = np.dot(X, true_coef)

# 약간의 노이즈를 더합니다
y += 5 * np.random.normal(size=(n_samples,))

데이터를 훈련 세트와 테스트 세트로 분할합니다.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)

비음수 최소제곱법(Non-Negative least squares)을 적합합니다.

from sklearn.linear_model import LinearRegression

reg_nnls = LinearRegression(positive=True)
y_pred_nnls = reg_nnls.fit(X_train, y_train).predict(X_test)
r2_score_nnls = r2_score(y_test, y_pred_nnls)
print("NNLS R2 score", r2_score_nnls)

출력:

NNLS R2 score 0.8225220806196526

OLS를 적합합니다.

reg_ols = LinearRegression()
y_pred_ols = reg_ols.fit(X_train, y_train).predict(X_test)
r2_score_ols = r2_score(y_test, y_pred_ols)
print("OLS R2 score", r2_score_ols)

출력:

OLS R2 score 0.7436926291700356

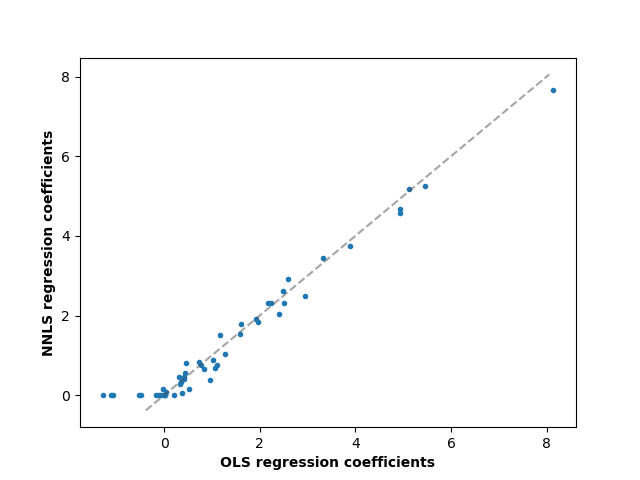
OLS와 NNLS 사이의 회귀 계수를 비교하면, 그들이 매우 상관됨을 관찰할 수 있지만(점선은 항등 관계(identity relation)입니다), 비음수 제약은 무언가를 0으로 수축합니다. 비음수 최소제곱법은 본질적으로 희소한 결과를 만들어냅니다.

fig, ax = plt.subplots()
ax.plot(reg_ols.coef_, reg_nnls.coef_, linewidth=0, marker=".")

low_x, high_x = ax.get_xlim()
low_y, high_y = ax.get_ylim()
low = max(low_x, low_y)
high = min(high_x, high_y)
ax.plot([low, high], [low, high], ls="--", c=".3", alpha=0.5)
ax.set_xlabel("OLS regression coefficients", fontweight="bold")
ax.set_ylabel("NNLS regression coefficients", fontweight="bold")

출력:

Text(55.847222222222214, 0.5, 'NNLS regression coefficients')