원문: Linear Regression Example

선형 회귀 예제

아래의 예제는 이차원 플롯의 데이터 점을 설명하기 위해, diabetes 데이터셋의 첫 특성 하나만 사용합니다. 직선을 플롯에서 볼 수 있으며, 이는 데이터셋의 관측된 반응값과 선형 근사(linear approximation)로 예측한 반응값 사이의 잔차제곱합(the residual sum of squares)을 가장 최소화하는 직선을, 선형 회귀(linear regression)가 어떻게 그리고자 하는지 보여줍니다.

계수(coefficients), 잔차제곱합과 결정계수(the coefficient of determination) 또한 계산됩니다.

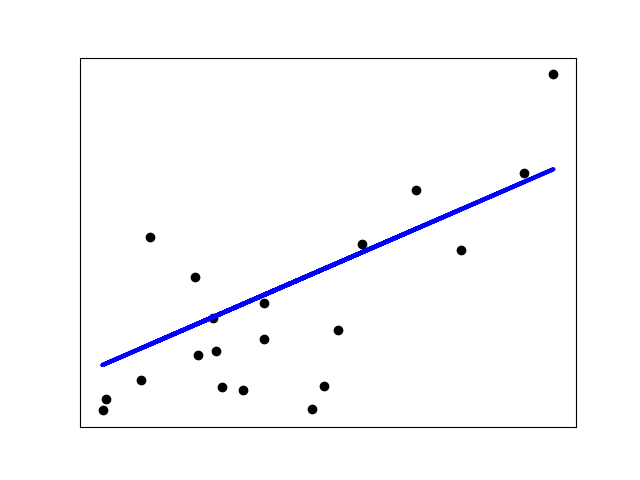
출력:

Coefficients:
 [938.23786125]
Mean squared error: 2548.07
Coefficient of determination: 0.47

# 코드 소스: Jaques Grobler
# 라이선스: BSD 3 clause

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

# 당뇨병 데이터셋을 불러옵니다
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)

# 단 하나의 특성만 사용합니다
diabetes_X = diabetes_X[:, np.newaxis, 2]

# 데이터를 훈련/테스트 세트로 분할합니다
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

# 목표값을 훈련/테스트 세트로 분할합니다
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]

# 선형 회귀 객체를 만듭니다
regr = linear_model.LinearRegression()

# 훈련 세트로 모델을 훈련시킵니다
regr.fit(diabetes_X_train, diabetes_y_train)

# 테스트 세트로 예측을 생성합니다
diabetes_y_pred = regr.predict(diabetes_X_test)

# 계수
print("Coefficients: \n", regr.coef_)
# 평균제곱오차(The mean squared error)
print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# 결정계수: 1이 완벽한 예측입니다
print("Coefficient of determination: %.2f" % r2_score(diabetes_y_test, diabetes_y_pred))

# 플롯 출력
plt.scatter(diabetes_X_test, diabetes_y_test, color="black")
plt.plot(diabetes_X_test, diabetes_y_pred, color="blue", linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()