원문: Unsupervised learning: seeking representations of the data

비지도 학습: 데이터 표현법 찾기

군집화: 관측을 함께 묶기

군집화에서 푸는 문제

붓꽃(iris) 데이터셋이 주어졌을 때, 3가지 유형의 붓꽃이 있다는 걸 알지만, 데이터셋에 레이블을 붙여줄 분류학자를 구할 수 없는 경우: 우리는 군집화(clustering) 작업을 시도해볼 수 있습니다: 관측을 군집(clusters)이라고 부르는 잘 구분된 집단으로 분할하는 것입니다.

K-평균 군집화

세상에는 아주 많은 군집화 기준 및 관련된 알고리즘이 있다는 걸 염두에 두세요. 가장 간단한 군집화 알고리즘은 K-평균(K-means)입니다.

>>> from sklearn import cluster, datasets
>>> X_iris, y_iris = datasets.load_iris(return_X_y=True)

>>> k_means = cluster.KMeans(n_clusters=3)
>>> k_means.fit(X_iris)
KMeans(n_clusters=3)
>>> print(k_means.labels_[::10])
[1 1 1 1 1 0 0 0 0 0 2 2 2 2 2]
>>> print(y_iris[::10])
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]

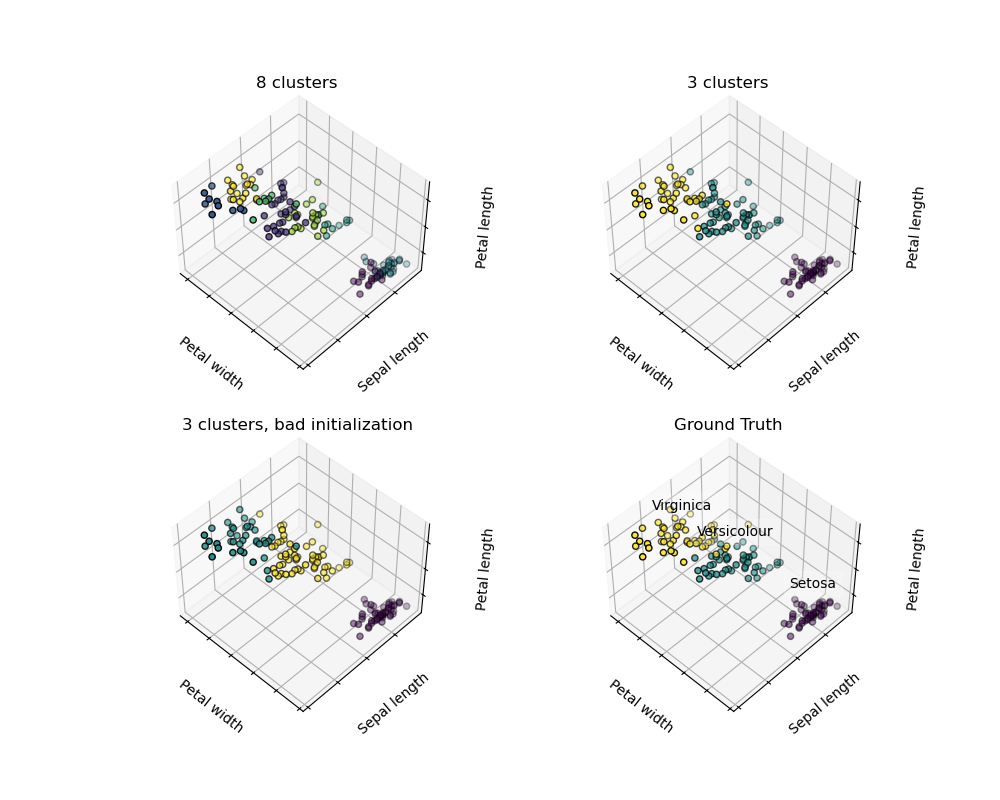
경고: 실제 정답(ground truth)을 복원한다는 보장은 절대 없습니다. 첫째로, 군집의 정확한 숫자를 고르는 것이 어렵습니다. 둘째로, 알고리즘은 초기화(initialization)에 민감하고, 사이킷런이 이 문제를 완화하기 위해 몇 가지 트릭을 사용하고는 있지만, 그럼에도 국소 최솟값(local minima)에 빠질 수 있습니다.
예를 들어, 위의 이미지에서, 우리는 실제 정답(오른쪽 아래 그림)과 다른 군집화 간의 차이를 관찰할 수 있습니다. 군집의 숫자가 너무 크거나(왼쪽 위 그림) 초기화가 잘못되었기 때문에(왼쪽 아래 그림), 예상한 레이블을 복원할 수 없습니다.
따라서 군집화 결과를 과도하게 해석(over-interpret)하지 않는 것이 중요합니다.

적용 예시: 벡터 양자화

일반적으로 군집화를, 특히 K평균을, 정보를 압축(compress)하기 위해 소수의 예제(exemplars)를 선택하는 기법으로 볼 수도 있습니다. 이 문제는 가끔 벡터 양자화(vector quantization)로 소개됩니다. 예를 들어, 이는 이미지를 포스터화(posterize)하는데 사용될 수 있습니다.

>>> import scipy as sp
>>> try:
...    face = sp.face(gray=True)
... except AttributeError:
...    from scipy import misc
...    face = misc.face(gray=True)
>>> X = face.reshape((-1, 1)) # (n_sample, n_feature) 배열이 필요합니다
>>> k_means = cluster.KMeans(n_clusters=5, n_init=1)
>>> k_means.fit(X)
KMeans(n_clusters=5, n_init=1)
>>> values = k_means.cluster_centers_.squeeze()
>>> labels = k_means.labels_
>>> face_compressed = np.choose(labels, values)
>>> face_compressed.shape = face.shape

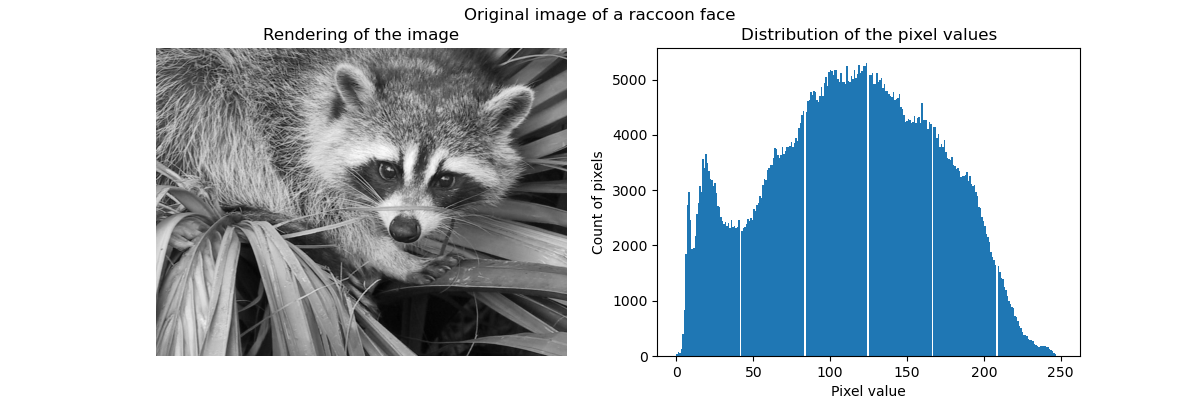
원시 이미지(raw image)

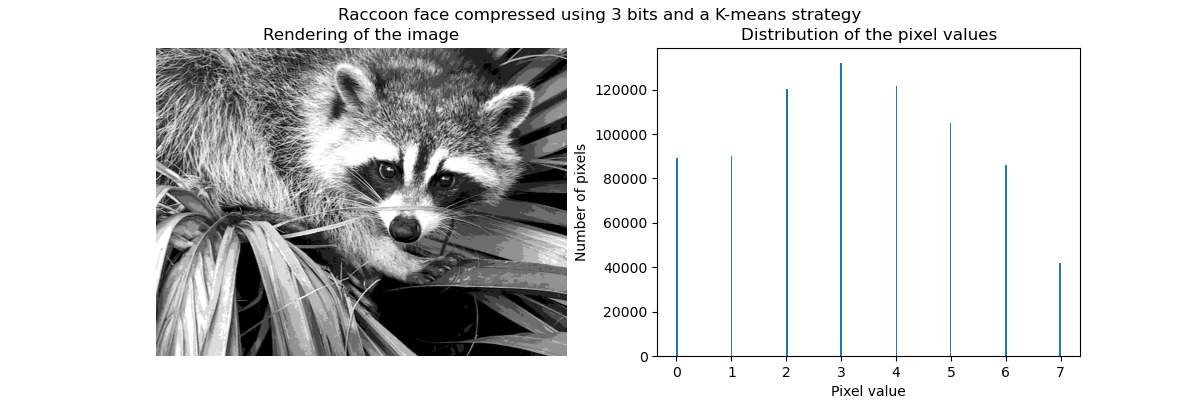
K-평균 양자화

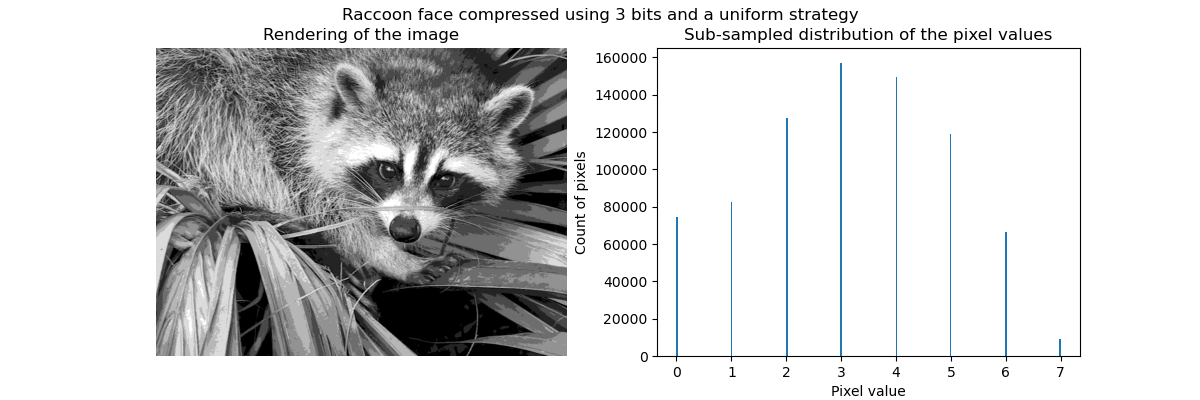
동일 분할(equal bins)

계층적 응집형 군집화: 와드

계층적 군집화(hierarchical clustering) 기법은 군집의 계층(hierarchy)을 쌓는 것이 목표인 군집 해석의 한 유형입니다. 일반적으로, 이 기술의 다양한 접근법은 다음 중 하나입니다:

연결 제약이 있는 군집화

응집형 군집화와 함께라면, 연결 그래프(connectivity graph)를 제공하여 어떤 표본들이 함께 군집화될지 지정해줄 수 있습니다. 사이킷런의 그래프는 인접 행렬(adjacency matrix)로 표현됩니다. 가끔은, 희소 행렬(sparse matrix)이 사용됩니다. 예를 들어, 이미지를 군집화할 때 연결된 구역(regions, 가끔 연결 성분(connected components)이라고도 함)을 되찾고자 할 경우 유용할 수 있습니다.

>>> from skimage.data import coins
>>> from scipy.ndimage import gaussian_filter
>>> from skimage.transform import rescale
>>> rescaled_coins = rescale(
...     gaussian_filter(coins(), sigma=2),
...     0.2, mode='reflect', anti_aliasing=False
... )
>>> X = np.reshape(rescaled_coins, (-1, 1))

우린 이미지의 벡터화된 버전이 필요합니다. 'rescaled_coins'는 처리 속도를 높이기 위해 동전 이미지를 축소한 버전입니다.

>>> from sklearn.feature_extraction import grid_to_graph
>>> connectivity = grid_to_graph(*rescaled_coins.shape)

데이터의 그래프 구조를 정의합니다. 픽셀(pixels)은 그 이웃에 연결되어 있습니다.

>>> n_clusters = 27  # 구역의 수

>>> from sklearn.cluster import AgglomerativeClustering
>>> ward = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward',
...                                connectivity=connectivity)
>>> ward.fit(X)
AgglomerativeClustering(connectivity=..., n_clusters=27)
>>> label = np.reshape(ward.labels_, rescaled_coins.shape)

특성 응집

우리는 차원의 저주(the curse of dimensionality), 즉 특성의 수에 비해 관측이 불충분한 양인 경우를 완화하기 위해 희소성을 사용할 수 있음을 보았습니다. 다른 접근법은 비슷한 특성을 합치는 것입니다: 특성 응집(feature agglomeration). 이 접근법은 특성 방향(direction)으로 군집화, 다른 말로 전치된(transposed) 데이터를 군집화함으로써 구현할 수 있습니다.

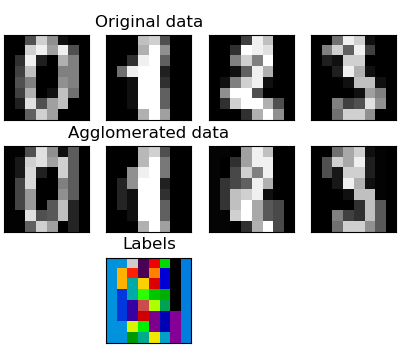
>>> digits = datasets.load_digits()
>>> images = digits.images
>>> X = np.reshape(images, (len(images), -1))
>>> connectivity = grid_to_graph(*images[0].shape)

>>> agglo = cluster.FeatureAgglomeration(connectivity=connectivity,
...                                      n_clusters=32)
>>> agglo.fit(X)
FeatureAgglomeration(connectivity=..., n_clusters=32)
>>> X_reduced = agglo.transform(X)

>>> X_approx = agglo.inverse_transform(X_reduced)
>>> images_approx = np.reshape(X_approx, images.shape)

transform과 inverse_transform 메서드

몇몇 추정기는 transform 메서드를 노출하는데, 이는 예를 들어 데이터셋의 차원을 감소시킵니다.

분해: 신호부터 성분과 부하량까지

성분(componenets)과 부하량(loadings)

X가 다변량 데이터라면, 우리가 풀고자 하는 문제는 그걸 다른 관측 기저(basis) 위에서 다시 쓰는 것입니다: 우리는 X = L C가 되게 하는 부하량 L과 성분 C의 집합을 학습하려고 합니다. 성분을 고르기 위한 여러 기준이 존재합니다.

주성분 분석: PCA

주성분 분석(principal component analysis, PCA)은 신호(signal)의 최대 분산(variance)을 설명하는 성공적인 성분을 선택합니다.

관측값들에 걸쳐 있는 점 구름(point cloud)은 한 방향으로 매우 평평합니다: 세 일변량(univariate) 특성 중 하나는 다른 둘에 비해 거의 정확하게 계산할 수 있습니다. PCA는 데이터가 평평하지 않은 방향을 찾습니다.

데이터를 변환하는데 사용할 경우, PCA는 주 부분공간(principal subspace)에 데이터를 투영(projecting)함으로써 차원을 감소시킬 수 있습니다.

>>> # 2개의 쓸만한 차원만 있는 신호를 만듭니다.
>>> x1 = np.random.normal(size=100)
>>> x2 = np.random.normal(size=100)
>>> x3 = x1 + x2
>>> X = np.c_[x1, x2, x3]

>>> from sklearn import decomposition
>>> pca = decomposition.PCA()
>>> pca.fit(X)
PCA()
>>> print(pca.explained_variance_)
[  2.18565811e+00   1.19346747e+00   8.43026679e-32]

>>> # 보시다시피, 2개의 첫 성분만 쓸만합니다.
>>> pca.n_components = 2
>>> X_reduced = pca.fit_transform(X)
>>> X_reduced.shape
(100, 2)

독립 성분 분석: ICA

독립 성분 분석(independent component analysis, ICA)은 부하량이 독립 정보량(amount of independent information)의 최대값을 갖게끔 성분을 선택합니다. 비가우시안(non-Gaussian) 독립 신호를 복원하는 것이 가능합니다:

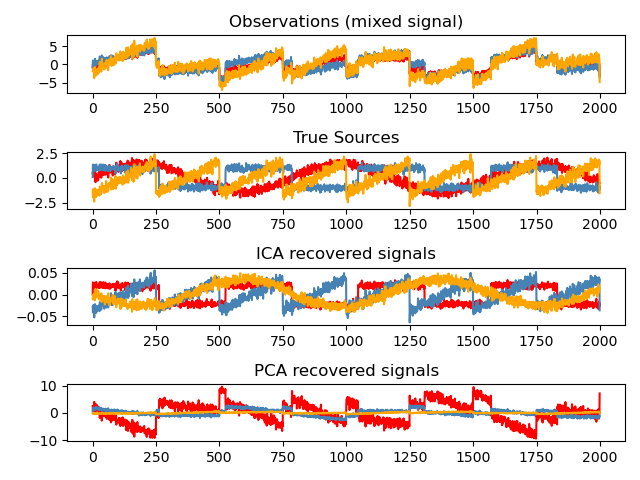
>>> # 표본 데이터를 생성합니다
>>> import numpy as np
>>> from scipy import signal
>>> time = np.linspace(0, 10, 2000)
>>> s1 = np.sin(2 * time)  # 신호 1번: 정현파(sinusoidal) 신호
>>> s2 = np.sign(np.sin(3 * time))  # 신호 2번: 사각파(square) 신호
>>> s3 = signal.sawtooth(2 * np.pi * time)  # 신호 3번: 톱니파(saw tooth) 신호
>>> S = np.c_[s1, s2, s3]
>>> S += 0.2 * np.random.normal(size=S.shape)  # 잡음(noise)을 더합니다
>>> S /= S.std(axis=0)  # 데이터를 표준화(standardize)합니다
>>> # 데이터를 섞습니다
>>> A = np.array([[1, 1, 1], [0.5, 2, 1], [1.5, 1, 2]])  # 행렬을 섞습니다
>>> X = np.dot(S, A.T)  # 관측을 생성합니다

>>> # ICA를 계산하기
>>> ica = decomposition.FastICA()
>>> S_ = ica.fit_transform(X)  # 추정되는 원천(sources)를 가져옵니다
>>> A_ = ica.mixing_.T
>>> np.allclose(X,  np.dot(S_, A_) + ica.mean_)
True