1.1. 선형 모델
다음은 목표값이 특성의 선형 결합(linear combination)일 것이라 기대하는 회귀(regression)를 위한 방법들입니다. 수학적 표기법으로, 만약 $\hat{y}$이 예측값이라면,
\[\hat{y}(w, x) = w_0 + w_1 x_1 + ... + w_p x_p\]모듈 전체에서, 벡터 $w = (w_1, …, w_p)$를 coef_, $w_0$를 intercept_로 선언합니다.
일반화 선형 모델(generalized linear models)로 분류를 수행하려면, 로지스틱 회귀를 보세요.
1.1.1. 최소제곱법
LinearRegression은 데이터셋의 관측된 목표값과 선형 근사(linear approximation)로 예측된 목표값 사이의 잔차제곱합(residual sum of squares)을 최소화하면서, 계수(coefficients) $w = (w_1, …, w_p)$로 선형 모델을 적합합니다. 수학적으로 이러한 형식의 문제를 해결합니다:
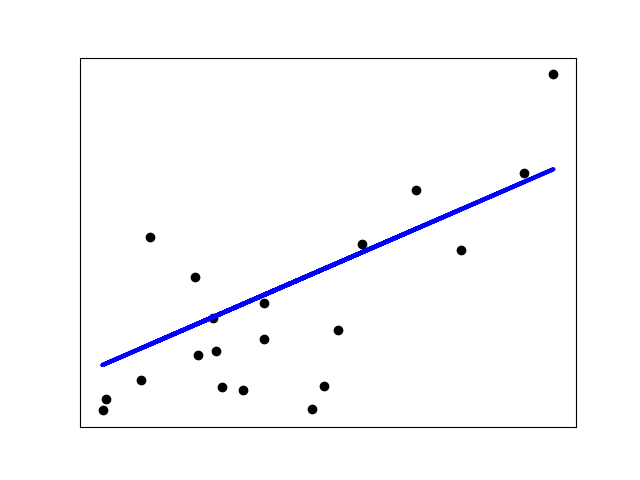
LinearRegression은 fit 메서드에 배열 X와 y를 받고, 선형 모델의 계수 $w$를 coef_ 멤버로 저장할 것입니다:
>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression()
>>> reg.coef_
array([0.5, 0.5])
최소제곱법(Ordinary Least Squares)에 의한 계수 추정은 특성들의 독립성에 의존합니다. 특성들이 상관되고 설계 행렬(design matrix) $X$의 열들이 근사적으로 선형 종속성을 가지면, 설계 행렬은 특이(singular) 행렬에 가까워지고, 그 결과로 최소제곱 추정치는 관측된 목표값의 무작위 오류에 매우 민감해지며, 큰 분산을 만듭니다. 이러한 다중공선성(multicollinearity) 상황은, 예를 들어 데이터가 실험 설계 없이 수집될 때 발생할 수 있습니다.
예제:
1.1.1.1. 비음수 최소제곱법
모든 계수를 비음수(non-negative)로 제약하는 것이 가능하며, (빈도 수나 상품 가격처럼) 물리적이나 자연적으로 비음수인 수량을 표현할 때 유용할 것입니다. LinearRegression은 불리언(boolean) positive 매개변수를 받습니다: True로 지정하면 비음수 최소제곱법이 적용됩니다.
예제:
1.1.1.2. 최소제곱법 복잡도
최소제곱법 해결책은 X의 특잇값분해(singular value decomposition)를 사용해 계산됩니다. 만약 X가 (n_samples, n_features) 형태의 행렬이라면 이 방법은 $n_{\text{samples}} \geq n_{\text{features}}$을 가정하여, $O(n_{\text{samples}} n_{\text{features}}^2)$의 비용이 듭니다.