원문: Supervised learning: predicting an output variable from high-dimensional observations
지도 학습: 고차원 관측으로부터 출력 변수 예측하기
지도 학습에서 해결하는 문제
지도 학습(supervised learning)은 두 데이터셋(datasets) 사이의 연결고리에 대한 학습으로 이루어집니다: 두 데이터셋은 관측(observed) 데이터 X와 목표값(target) 또는 레이블(labels)이라고 보통 부르는, 예측하고자 하는 외부 변수 y입니다. 대부분, y는 n_samples(표본 수) 길이의 1차원 배열(1D array)입니다.
사이킷런의 모든 지도 추정기(estimators)는 모델(model)에 적합(fit)하기 위한 fit(X, y) 메서드(method)와 레이블 없는 관측 X을 받아 예측 레이블 y를 반환하는 predict(X) 메서드를 구현합니다.
어휘: 분류와 회귀
만약 예측 작업이 관측값을 유한한 레이블 집합 안에서 분류하는 것이라면, 다른 말로 관측된 개체에 “이름을 붙이는(name)” 것이라면, 작업은 분류(classification) 작업이라고 부릅니다. 반면에, 목표가 연속적인 목표 변수를 예측하는 거라면, 회귀(regression) 작업이라고 부릅니다.
사이킷런에서 분류를 할 때, y는 정수(integers) 또는 문자열(strings)의 벡터(vector)입니다.
참고: 사이킷런에서 사용하는 기초 기계 학습 어휘에 대해 빠르게 훑어보려면 사이킷런과 함께 하는 기계 학습 입문를 보세요.
최근접 이웃과 차원의 저주
붓꽃 분류하기
붓꽃(iris) 데이터셋은 붓꽃의 꽃잎(petal)과 꽃받침(sepal)의 길이(length)와 너비(width)에서 붓꽃의 3가지 유형(Setosa, Versicolour, 그리고 Verginica)을 식별하는 것으로 이루어지는 분류 작업입니다.
>>> import numpy as np
>>> from sklearn import datasets
>>> iris_X, iris_y = datasets.load_iris(return_X_y=True)
>>> np.unique(iris_y)
array([0, 1, 2])
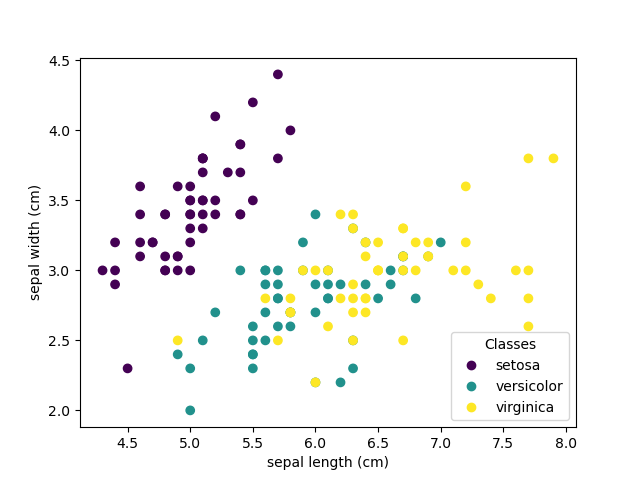
k-최근접 이웃 분류기
가장 간단한 가능한 분류기는 최근접 이웃(nearest neighbor)입니다: 새로운 관측 X_test이 주어지면, 훈련 세트(training set, 즉 추정기를 훈련하기 위해 사용한 데이터)에서 가장 가까운 특성 벡터(feature vector)가 있는 관측값을 찾는 것입니다. (이 유형의 분류기에 대한 더 많은 정보를 원하신다면 온라인 사이킷런 문서의 최근접 이웃 섹션을 보세요.)
훈련 세트와 테스트 세트
학습 알고리즘을 실험할 때, 추정기를 적합할 때 사용한 데이터로 추정기의 예측력을 테스트하지 않는 것이 중요합니다, 왜냐하면 이게 새 데이터(new data)에 대한 추정기의 성능을 평가하지는 못할 것이기 때문입니다. 이것이 종종 데이터셋을 훈련(train)과 테스트(test) 데이터로 나누는 이유입니다.
**KNN(k 최근접 이웃) 분류 예제:
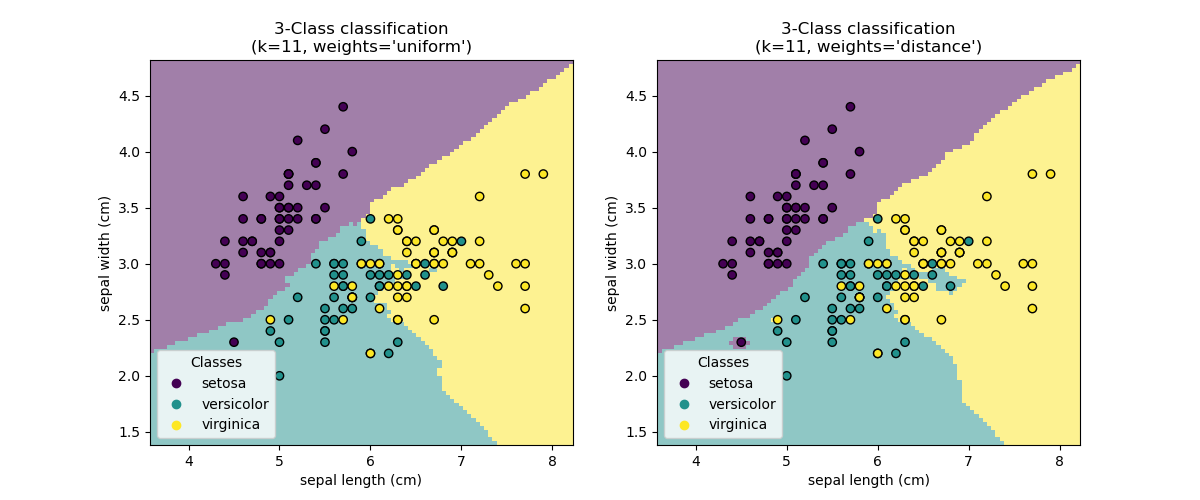
>>> # 붓꽃 데이터를 훈련과 테스트 세트로 나눕니다
>>> # 데이터를 무작위로 나누기 위한 무작위 순열(random permutation)
>>> np.random.seed(0)
>>> indices = np.random.permutation(len(iris_X))
>>> iris_X_train = iris_X[indices[:-10]]
>>> iris_y_train = iris_y[indices[:-10]]
>>> iris_X_test = iris_X[indices[-10:]]
>>> iris_y_test = iris_y[indices[-10:]]
>>> # 최근접-이웃 분류기를 만들고 적합합니다
>>> from sklearn.neighbors import KNeighborsClassifier
>>> knn = KNeighborsClassifier()
>>> knn.fit(iris_X_train, iris_y_train)
KNeighborsClassifier()
>>> knn.predict(iris_X_test)
array([1, 2, 1, 0, 0, 0, 2, 1, 2, 0])
>>> iris_y_test
array([1, 1, 1, 0, 0, 0, 2, 1, 2, 0])
차원의 저주
추정기가 효과적이기 위해서는, 문제에 따라 달라지는 어떤 값 $d$ 보다, 이웃하는 점들 사이의 거리가 작도록 해야합니다. 일차원에서는, 평균적으로 $n \sim 1/d$ 의 점이 필요합니다. 위 $k$-NN 예제의 맥락에서는, 만약 데이터가 0부터 1까지의 범위이며 $n$ 개의 훈련 관측값이 있는 딱 하나의 특성으로 설명된다면, 새로운 데이터는 $1/n$ 보다 멀리 떨어져있으면 안됩니다. 따라서 최근접 이웃 결정 규칙은 $1/n$ 이 클래스간 특성 다양성(feature variations)의 규모에 비해 작을수록 효율적일 것입니다.
특성의 개수가 $p$ 라면, 여러분은 $n \sim 1/{d}^p$ 의 점이 필요합니다. 우리가 일차원에 10개의 점이 필요하다고 해봅시다: 이제 $[0, 1]$ 공간(space)을 덮으려면 $p$ 차원에서 ${10}^p$ 개의 점이 필요합니다. $p$ 가 커질수록, 좋은 추정기를 위해서 필요한 훈련 점의 개수는 지수적(exponentially)으로 증가합니다.
예를 들어, 각 점이 그냥 단일 숫자(8 바이트(bytes))라면, 소소한 $p \sim 20$ 차원에서의 효과적인 $k$-NN 추정기조차 전체 인터넷의 현재 추정 크기(±1000 엑사바이트(Exabytes)쯤)보다 더 많은 훈련 데이터를 필요로 할 것입니다.
이것을 차원의 저주(the curse of dimensionality)라 부르고 기계 학습이 다루는 핵심 문제입니다.
선형 모델: 회귀부터 희소성까지
당뇨병 데이터셋
당뇨병(diabetes) 데이터셋은 442명의 환자에게서 측정된 10개의 생리학적 변수(연령(age), 성별(sex), 체중(weight), 혈압(blood pressure))와, 일 년 후의 질병 진행 지표(an indication of disease progression)로 구성되어 있습니다:
>>> diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
>>> diabetes_X_train = diabetes_X[:-20]
>>> diabetes_X_test = diabetes_X[-20:]
>>> diabetes_y_train = diabetes_y[:-20]
>>> diabetes_y_test = diabetes_y[-20:]
주어진 작업은 생리학적 변수로부터 질병 진행을 예측하는 것입니다.
선형 회귀
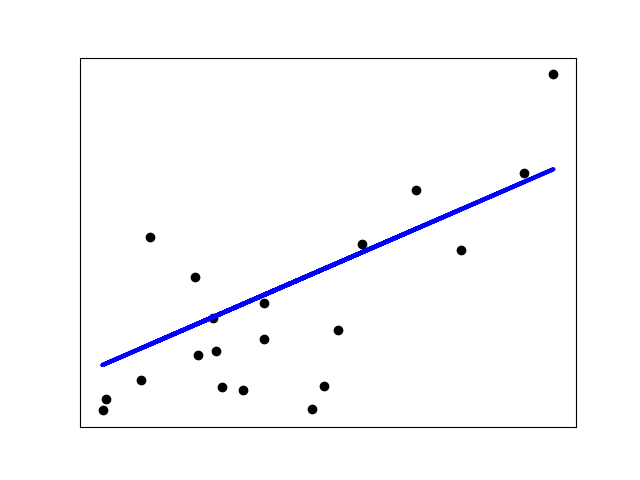
LinearRegression(선형 회귀)은, 가장 간단한 형태로, 모델의 잔차 제곱(squared residuals)의 합을 가능한 가장 작게 만들기 위해 매개변수(parameters) 집합을 조정하여 선형 모델(linear model)을 데이터 세트에 적합합니다.
선형 모델: $y = X \beta + \epsilon$
- $X$: 데이터
- $y$: 목표 변수
- $\beta$: 계수(coefficients)
- $\epsilon$: 관찰 잡음(noise)
>>> from sklearn import linear_model
>>> regr = linear_model.LinearRegression()
>>> regr.fit(diabetes_X_train, diabetes_y_train)
LinearRegression()
>>> print(regr.coef_)
[ 0.30349955 -237.63931533 510.53060544 327.73698041 -814.13170937
492.81458798 102.84845219 184.60648906 743.51961675 76.09517222]
>>> # 평균 제곱 오차(mean square error)
>>> np.mean((regr.predict(diabetes_X_test) - diabetes_y_test)**2)
2004.5...
>>> # 설명되는 분산(variance) 점수: 1은 완벽한 예측이며
>>> # 0은 X와 y 사이에 선형 연관관계(linear relationship)가
>>> # 없다는 의미입니다.
>>> regr.score(diabetes_X_test, diabetes_y_test)
0.585...
수축
만약 차원마다 거의 데이터 점이 없다면, 관측 속의 잡음은 높은 분산을 유도합니다:
>>> X = np.c_[ .5, 1].T
>>> y = [.5, 1]
>>> test = np.c_[ 0, 2].T
>>> regr = linear_model.LinearRegression()
>>> import matplotlib.pyplot as plt
>>> plt.figure()
<...>
>>> np.random.seed(0)
>>> for _ in range(6):
... this_X = .1 * np.random.normal(size=(2, 1)) + X
... regr.fit(this_X, y)
... plt.plot(test, regr.predict(test))
... plt.scatter(this_X, y, s=3)
LinearRegression...
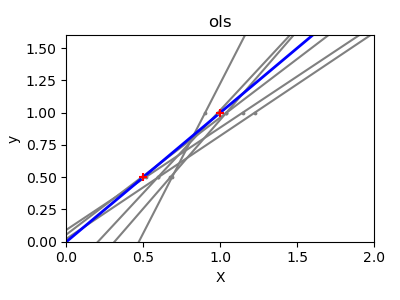
고차원 통계적 학습(high-dimensional statistical learning)의 해결책은 회귀 계수를 0으로 수축(shrink)하는 것입니다: 무작위로 고른 두 관측값의 집합 중 어떤 것이라도 상관관계가 없을 수 있는 것입니다. 이를 Ridge(릿지) 회귀라고 합니다.
>>> regr = linear_model.Ridge(alpha=.1)
>>> plt.figure()
<...>
>>> np.random.seed(0)
>>> for _ in range(6):
... this_X = .1 * np.random.normal(size=(2, 1)) + X
... regr.fit(this_X, y)
... plt.plot(test, regr.predict(test))
... plt.scatter(this_X, y, s=3)
Ridge...
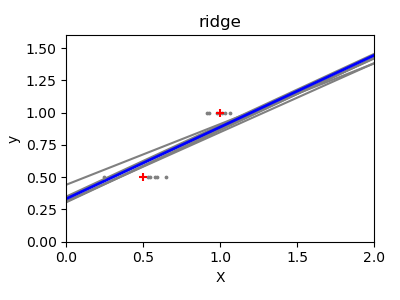
이건 편향/분산 트레이드오프(bias/variance tradeoff)의 예입니다: 릿지 alpha 매개변수가 클수록, 편향은 높아지고 분산은 낮아집니다.
우리는 누락 오차(left out error)를 최소화하기 위해 alpha를 선택할 수 있는데요, 이번엔 인공적인 데이터보다는 당뇨병 데이터셋을 사용합니다:
>>> alphas = np.logspace(-4, -1, 6)
>>> print([regr.set_params(alpha=alpha)
... .fit(diabetes_X_train, diabetes_y_train)
... .score(diabetes_X_test, diabetes_y_test)
... for alpha in alphas])
[0.585..., 0.585..., 0.5854..., 0.5855..., 0.583..., 0.570...]
참고: 적합된 매개변수 잡음을 잡아서 모델이 새로운 데이터에 일반화되는 것을 막는 걸 과대적합(overfitting)이라고 합니다. 릿지 회귀로 도입된 편향은 정규화(regularization)라고 합니다.
희소성
딱 특성 1과 2만 적합하기
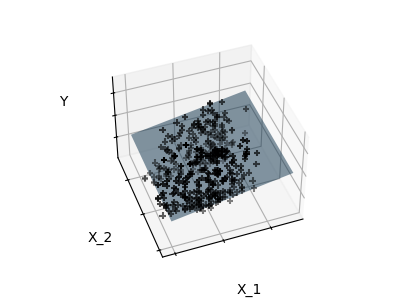
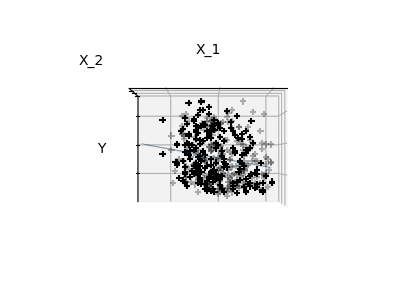
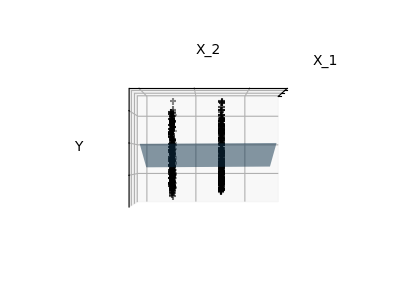
참고: 전체 당뇨병 데이터셋을 표현하는 것은 11 차원을 포함합니다(10개 특성 차원과 하나의 목표 번수). 이러한 표현에 대한 직관을 발달시키는 건 어렵지만, 상당히 비어있는 공간이 될 거란걸 염두에 두는 것은 유용할 수 있습니다.
보다시피, 특성 2번이 전체 모델에서는 강력한 계수를 갖지만, 특성 1번과 함께 고려되었을 때는 y에 대해 작은 정보만을 전달합니다.
이 문제의 조건을 개선하기 위해(즉 차원의 저주를 완화하기 위해), 유익한(informative) 특성만 선택하고, 특성 2번처럼 유익하지 않은(non-informative) 것들은 0으로 설정하는 것이 꽤나 흥미로울 것입니다. 하지만 릿지 회귀는 그들의 기여를 감소시키되, 0으로 설정하지는 않습니다. 다른 벌칙 접근법(penalization approach)인 라쏘(Lasso)(least absolute shrinkage and selection operator)는, 일부 계수를 0으로 설정할 수 있습니다. 이러한 기법을 희소 기법(sparse methods)이라 부르며 희소성(sparsity)은 오컴의 면도날(Occam’s razor): 더 간단한 모델을 선호하는 것을 적용하는 것으로 볼 수 있습니다.
>>> regr = linear_model.Lasso()
>>> scores = [regr.set_params(alpha=alpha)
... .fit(diabetes_X_train, diabetes_y_train)
... .score(diabetes_X_test, diabetes_y_test)
... for alpha in alphas]
>>> best_alpha = alphas[scores.index(max(scores))]
>>> regr.alpha = best_alpha
>>> regr.fit(diabetes_X_train, diabetes_y_train)
Lasso(alpha=0.025118864315095794)
>>> print(regr.coef_)
[ 0. -212.4... 517.2... 313.7... -160.8...
-0. -187.1... 69.3... 508.6... 71.8... ]
같은 문제를 위한 다른 알고리즘
같은 수학 문제를 풀기 위해 다른 알고리즘을 사용할 수 있습니다. 예를 들어 사이킷런의 Lasso 객체는, 큰 데이터셋에서 효율적인 좌표 하강(coordinate descent) 기법으로 라쏘 회귀 문제를 풉니다. 하지만, 사이킷런은 LARS 알고리즘을 사용하는 LassoLars 객체도 제공하며, 이는 추정된 가중치 벡터(weight vector)가 매우 희소한 문제들(즉 아주 관측값이 적은 문제들)에 매우 효율적입니다.
분류
붓꽃 레이블 작업 같은 분류를 위해, 선형 회귀는 결정 경계(decision frontier)에서 멀리 떨어진 데이터에 너무 많은 가중치를 줄 것이기 때문에 좋은 접근법이 아닙니다. 선형 접근법은 시그모이드(sigmoid) 함수 또는 로지스틱(logistic) 함수에 적합하는 것입니다:
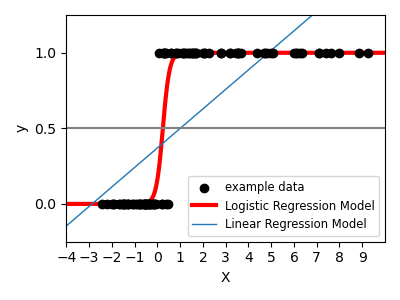
$y = \textrm{sigmoid}(X\beta - \textrm{offset}) + \epsilon = \frac{1}{1 + \textrm{exp}(- X\beta + \textrm{offset})} + \epsilon$
>>> log = linear_model.LogisticRegression(C=1e5)
>>> log.fit(iris_X_train, iris_y_train)
LogisticRegression(C=100000.0)
이는 LogisticRegression(로지스틱 회귀)이라 합니다.
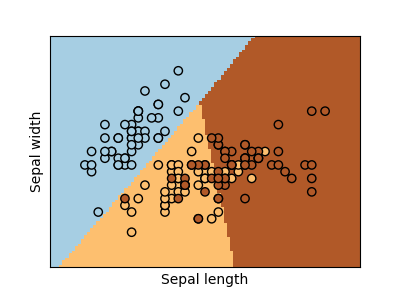
다중클래스(multiclass) 분류
만약 여러분이 예측할 클래스가 여러 개라면, 일대다(one-versus-all) 분류기를 적합한 다음 최종 결정을 위한 투표 휴리스틱(voting heuristic)을 사용하는 것이 자주 사용되는 옵션입니다.
로지스틱 회귀에서의 축소와 희소성
LogisticRegression 객체에서 C 매개변수는 정규화의 양을 조절합니다: 큰 C 값은 정규화가 적어집니다. penalty="l2"는 수축을 주며(즉 희소하지 않은 계수), penalty="l1"은 희소성을 줍니다.
연습
최근접 이웃과 선형 모델로 숫자(digits) 데이터셋을 분류해보세요. 마지막 10%를 제외하고 이 관측들에 대한 예측 성능을 테스트하세요.
from sklearn import datasets, neighbors, linear_model
X_digits, y_digits = datasets.load_digits(return_X_y=True)
X_digits = X_digits / X_digits.max()
정답지는 여기에서 다운로드할 수 있습니다.
서포트 벡터 머신(SVMs)
선형 SVMs
서포트 벡터 머신(Support Vector Machines)은 판별(discriminant) 모델군에 속합니다: 그들은 두 클래스 사이의 마진(margin)을 최대화하는 평면(plane)을 구축하는 표본의 조합을 찾고자 합니다. 정규화는 C 매개변수로 설정합니다: 작은 C 값은 마진이 분리하는 선 주위의 많거나 또는 모든 관측을 사용해 계산된다는 것을 의미합니다(많은 정규화); 큰 C 값은 마진이 분리하는 선에 가까운 관측을 사용해 계산된다는 것을 의미합니다(적은 정규화).
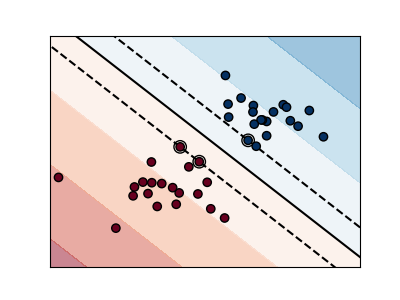
정규화되지 않은 SVM
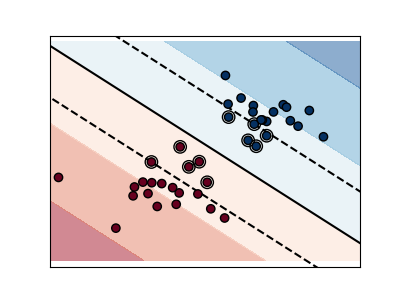
정규화된 SVM(기본값)
예제:
SVM은 회귀에서도 -SVR(서포트 벡터 회귀)(Support Vector Regression), 분류에서도 -SVC(서포트 벡터 분류)(Support Vector Classification)- 사용할 수 있습니다.
>>> from sklearn import svm
>>> svc = svm.SVC(kernel='linear')
>>> svc.fit(iris_X_train, iris_y_train)
SVC(kernel='linear')
**경고: 데이터 정규화하기(normalizing)
SVM을 포함한 많은 추정기들에게, 각 특성에 대해 단위 표준 편차(unit standard deviation)가 있는 데이터셋을 갖는 것이 좋은 예측값을 얻기 위해 중요합니다.
커널 사용
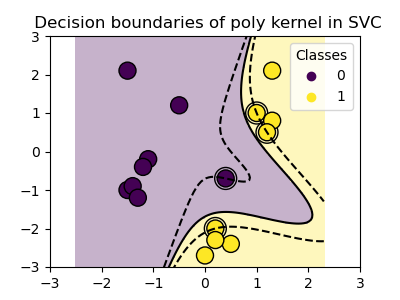
클래스들은 특성 공간에서 항상 선형적으로 분리 가능(linearly separable)하지는 않습니다. 해결책은 선형은 아니지만 대신에 다항식(polynomial)일 수 있는 결정 함수(decision function)를 구축하는 것입니다. 이는 커널(kernels)을 관측값에 배치하여 결정 에너지(decision energy)를 만드는 것처럼 보이는 커널 트릭(kernel trick)을 사용하여 수행합니다.
선형 커널
>>> svc = svm.SVC(kernel='linear')
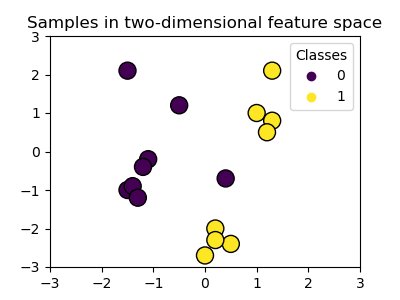
다항식 커널
>>> svc = svm.SVC(kernel='poly',
... degree=3)
>>> # degree(차수): 다항식 차수
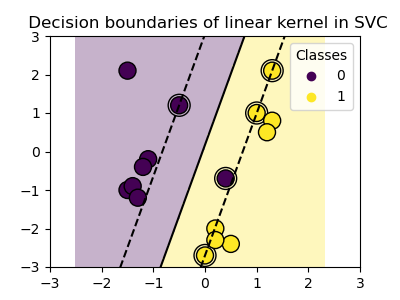
RBF 커널(Radial Basis Function(방사기저함수))
>> svc = svm.SVC(kernel='rbf')
>>> # gamma(감마): 방사 커널의
>>> # 크기의 역수
대화형 예제
svm_gui.py를 다운로드하려면 SVM GUI를 보세요; 우측과 좌측 버튼으로 각 클래스에 데이터 점을 더하고, 모델을 적합하고 매개변수와 데이터를 바꾸세요.
연습
2개의 첫 특성을 사용해, SVM으로 붓꽃 데이터셋에서 클래스 1번과 2번을 분류해보세요. 각 클래스의 마지막 10%를 제외하고 이 관측들에 대한 예측 성능을 테스트하세요.
경고: 클래스에 순서가 있으니, 전체 끝 10%를 제외하지는 마세요, 만약 그러면 여러분은 오직 한 클래스만 테스트하게 될 것입니다.
힌트: 직관을 얻기 위해 decision_function 메서드를 제공받아 사용할 수 있습니다.
X = iris.data
y = iris.target
X = X[y != 0, :2]
y = y[y != 0]

정답지는 여기에서 다운로드할 수 있습니다.